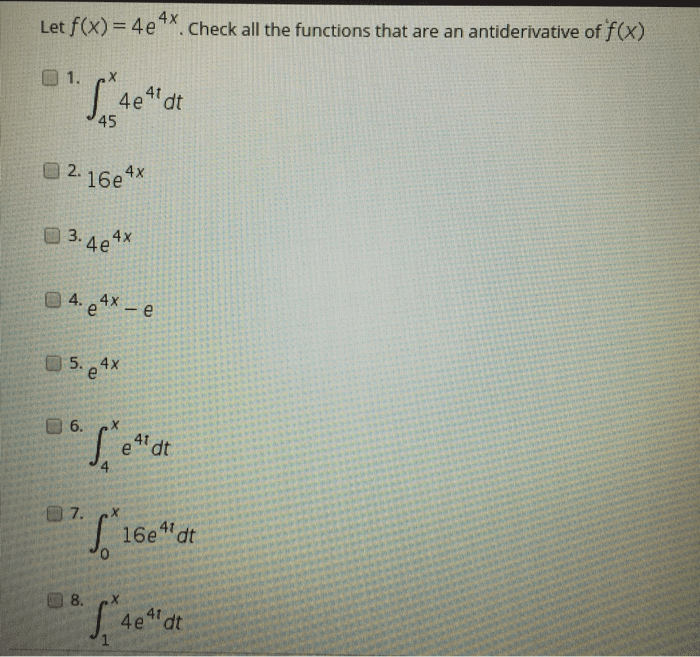CAS MA 121 Chapter 4: Chapter 4 Integration.docx

• School: Boston University
• Department: Mathematics & Statistics
• Course: CAS MA 121
• Professor: Panch

Document Summary

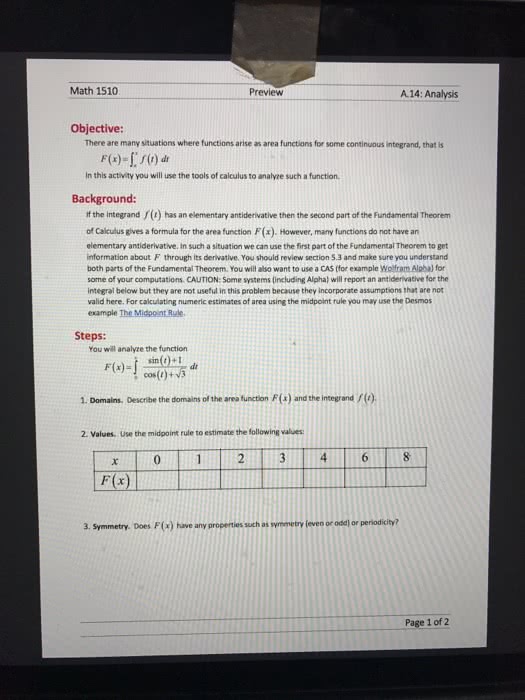
Sum and di erence: b a kf (x) dx = k b a f (x) dx b a (f (x) g(x)) dx = b a f (x) dx b a g(x) dx. Additivity: b a f (x) dx + c b f (x) dx = c a f (x) dx. F (x) = x a f (t) dt has a derivative at every point x in [a, b] and ddf dxdx x a f (t) dt = f (x). F (x + h) f (x) = x+h a f (t) dt x a f (t) dt = x+h x f (t) dt. = g(b) g(a) b a b a b a f (t) dt a a f (t) dt f (t) dt 0 f (t) dt. We can use u substitution in de nite integrals: b a f (g(x))g (x)dx = g(b) g(a) f (u) du where u = g(x), and du = g (x) dx.