1
answer
0
watching
45
views
13 Nov 2019
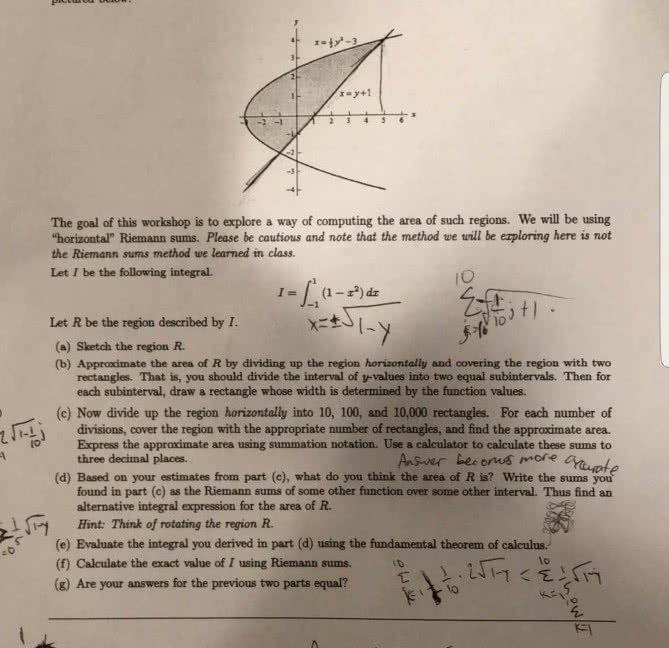
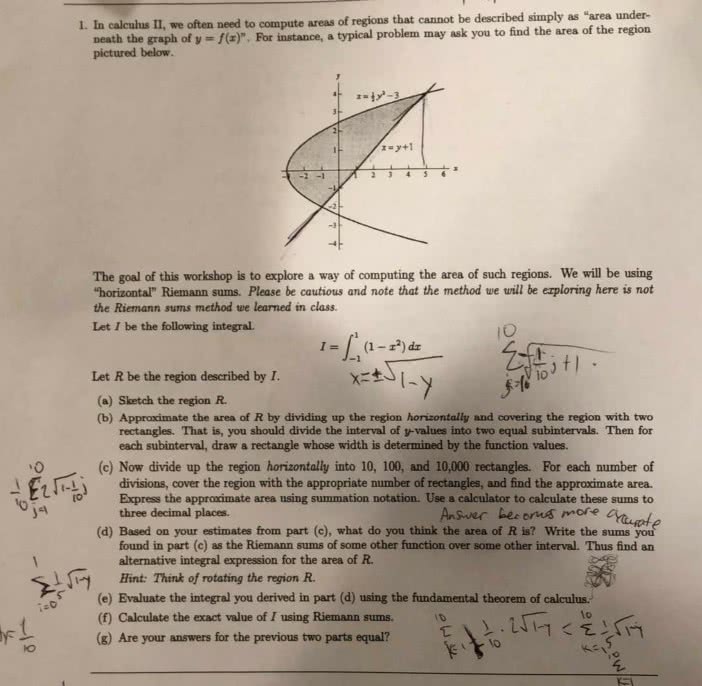
The number e can be defined as number along the x-axis for which, starting from x =1, the area under the curve y = 1/x from x = 1 to x = e is 1. Partitioning the interval [1,3] into sufficiently small subintervals, approximate the area under the y = 1/x over the interval in a way that allows you to conclude that 2 < e < 3. You will need to use enough subintervals and then do some arithmetic. Familiarity with a famous discrete series can save you time but, strictly speaking, is not needed for the numerical computation. (the problem here is to define e indepedently, in its own right, by only using the function y = 1/x and operations of calculus)
The number e can be defined as number along the x-axis for which, starting from x =1, the area under the curve y = 1/x from x = 1 to x = e is 1. Partitioning the interval [1,3] into sufficiently small subintervals, approximate the area under the y = 1/x over the interval in a way that allows you to conclude that 2 < e < 3. You will need to use enough subintervals and then do some arithmetic. Familiarity with a famous discrete series can save you time but, strictly speaking, is not needed for the numerical computation. (the problem here is to define e indepedently, in its own right, by only using the function y = 1/x and operations of calculus)
Jamar FerryLv2
3 Nov 2019
