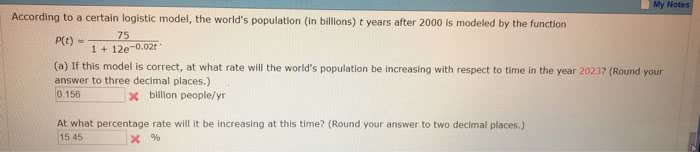
The population of the world was about 5.3 billion in 1990. Birth rates in the 1990s ranged from 35 to 40 million per year and death rates ranged from 15 to 20 million per year. Let's assume that the carrying capacity for world population is 120billion. (Assume that the difference in birth and death rates is 20 million/year = 0.02 billion/year.)
(a) Write the logistic differential equation for these data. (Because the initial population is small compared to the carrying capacity, you can take k to be an estimate of the initial relative growth rate. Let P be the population in billions and t be the time in years, where
t = 0
corresponds to 1990.)
dP/dt =
year 2100 P = year 2500 P =
=
(b) Use the logistic model to estimate the world population in the year 2000. Compare with the actual population of 6.1 billion. (Round the answer to two decimal places.)
P =
(c) Use the logistic model to predict the world population in the years 2100 and 2500. (Round your answer to two decimal places.)
(d) What are your predictions if the carrying capacity is 60 billion? (Round your answers to two decimal places.)
year 2000 P = year 2100 P = year 2500 P =
The population of the world was about 5.3 billion in 1990. Birth rates in the 1990s ranged from 35 to 40 million per year and death rates ranged from 15 to 20 million per year. Let's assume that the carrying capacity for world population is 120billion. (Assume that the difference in birth and death rates is 20 million/year = 0.02 billion/year.)
(a) Write the logistic differential equation for these data. (Because the initial population is small compared to the carrying capacity, you can take k to be an estimate of the initial relative growth rate. Let P be the population in billions and t be the time in years, where
t = 0
corresponds to 1990.)
dP/dt =
| year 2100 | P | = | ||
| year 2500 | P | = |
=
(b) Use the logistic model to estimate the world population in the year 2000. Compare with the actual population of 6.1 billion. (Round the answer to two decimal places.)
P =
(c) Use the logistic model to predict the world population in the years 2100 and 2500. (Round your answer to two decimal places.)
(d) What are your predictions if the carrying capacity is 60 billion? (Round your answers to two decimal places.)
| year 2000 | P | = | ||
| year 2100 | P | = | ||
| year 2500 | P | = |