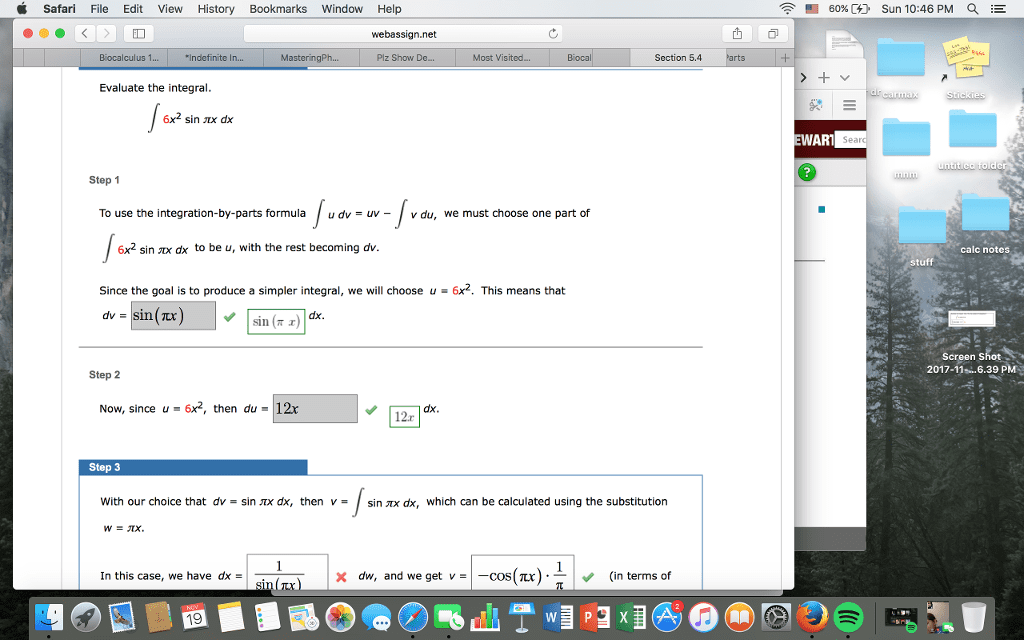
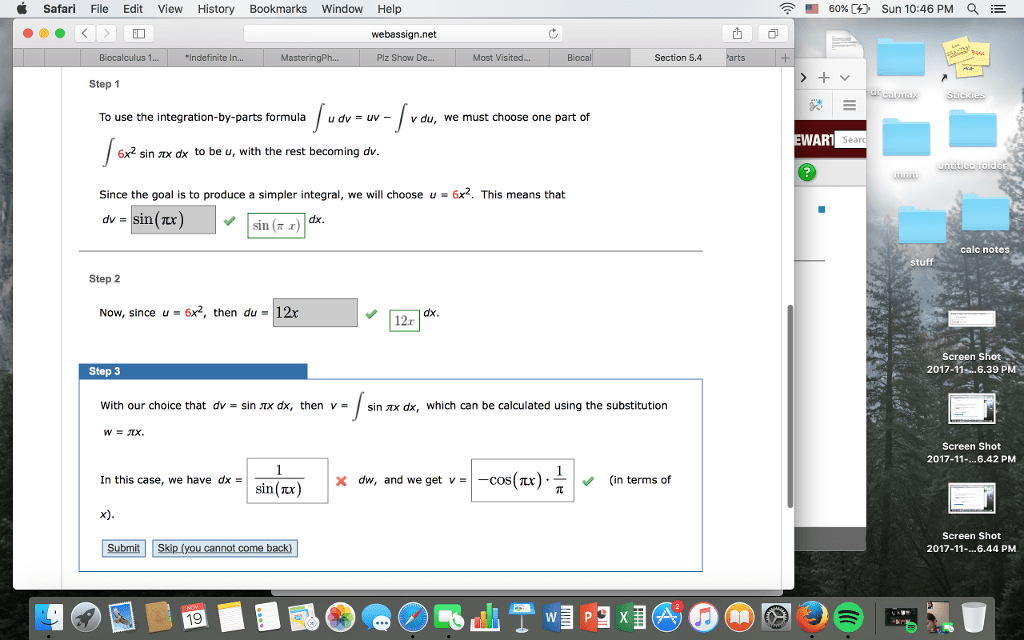
1
answer
0
watching
125
views
6 Nov 2019
Consider the integral â«[xsec2x] dx.
If we try to apply Integration by Parts, we have (at least) two choices.
(1) First, we can do
u=x dv=sec2xdx implying
du= Answer v= Answer
Then
â«[xsec2x] dx = Answer - â«tanx dx = xtanx + Answer + C
Hence, this choice of u and dv worked great.
(2) We could have tried
u=sec2x dv=xdx leading to
du=2sec2xAnswer v=(1/2)Answer
Then
â«[xsec2x] dx = (1/2)Answersec2x - â«[x2sec2xtanx] dx,
and the last integral seems (is) more complicated than the original one, â«[xsec2x] dx, hence, the second choice is not a good one.
Consider the integral â«[xsec2x] dx.
If we try to apply Integration by Parts, we have (at least) two choices.
(1) First, we can do
u=x dv=sec2xdx implying
du= Answer v= Answer
Then
â«[xsec2x] dx = Answer - â«tanx dx = xtanx + Answer + C
Hence, this choice of u and dv worked great.
(2) We could have tried
u=sec2x dv=xdx leading to
du=2sec2xAnswer v=(1/2)Answer
Then
â«[xsec2x] dx = (1/2)Answersec2x - â«[x2sec2xtanx] dx,
and the last integral seems (is) more complicated than the original one, â«[xsec2x] dx, hence, the second choice is not a good one.
Sixta KovacekLv2
29 Sep 2019