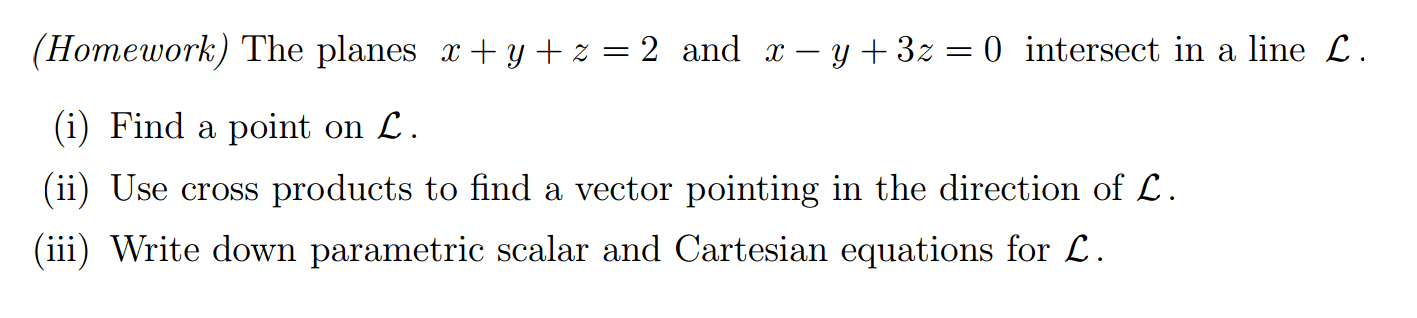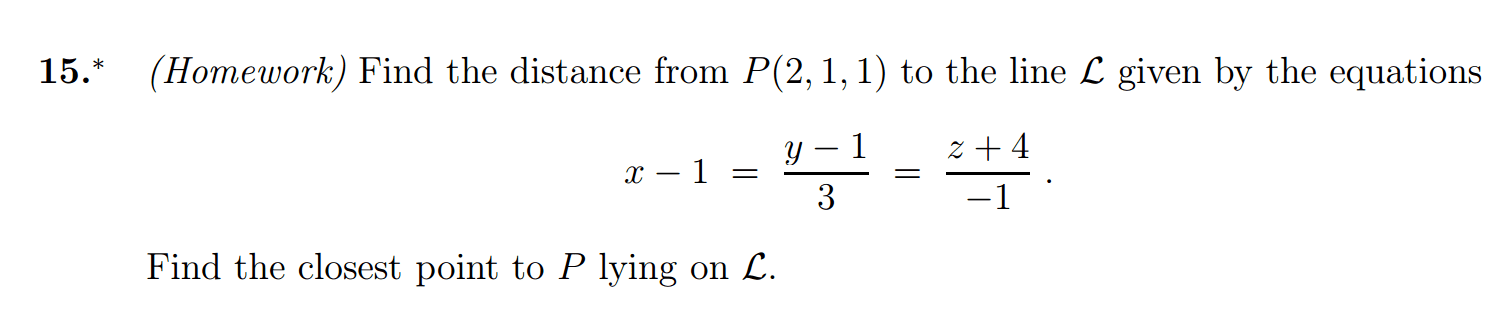Let L be the line in parametric form x = s + 1, y = s - 2, z = 2s + 3, where s 2 R, and
let P and P' be the planes with cartesian equations 3x - 2y + z = 1 and x - y - 2z = 1,
respectively.
(a) Show that P and P' intersect in a line L' and find its parametric form.
(b) Determine the angle between the two planes P and P'.
(c) Show that the two lines L and L' are skew.
(d) Find points p on L and p' on L' such that the distance between them is minimised.
Hint: This will occur when the line from p' to p is perpendicular to both L and L'. The detailed answer to this part is especially crucial for me to understand as it asks to find points p and p' on lines L and L' r4spectively such that the distance is minimised, not find the distance as such.. I asked this question previously but wasnt satisfied with the answer.
Let L be the line in parametric form x = s + 1, y = s - 2, z = 2s + 3, where s 2 R, and
let P and P' be the planes with cartesian equations 3x - 2y + z = 1 and x - y - 2z = 1,
respectively.
(a) Show that P and P' intersect in a line L' and find its parametric form.
(b) Determine the angle between the two planes P and P'.
(c) Show that the two lines L and L' are skew.
(d) Find points p on L and p' on L' such that the distance between them is minimised.
Hint: This will occur when the line from p' to p is perpendicular to both L and L'. The detailed answer to this part is especially crucial for me to understand as it asks to find points p and p' on lines L and L' r4spectively such that the distance is minimised, not find the distance as such.. I asked this question previously but wasnt satisfied with the answer.