ECON 6306 Lecture Notes - Lecture 6: Scatter Plot, Spurious Relationship, Statistical Significance

34 views2 pages

pearjellyfish746

7 May 2018

School

UT-Dallas

Department

Economics

Course

ECON 6306

Professor

Dr. Michael Tiefelsdorf

For unlimited access to Class Notes, a Class+ subscription is required.

Bivariate Regression

Regression is, in its simplest form, a technique to

find the strength of relationship between a

dependent (y) and independent (x). Consider the

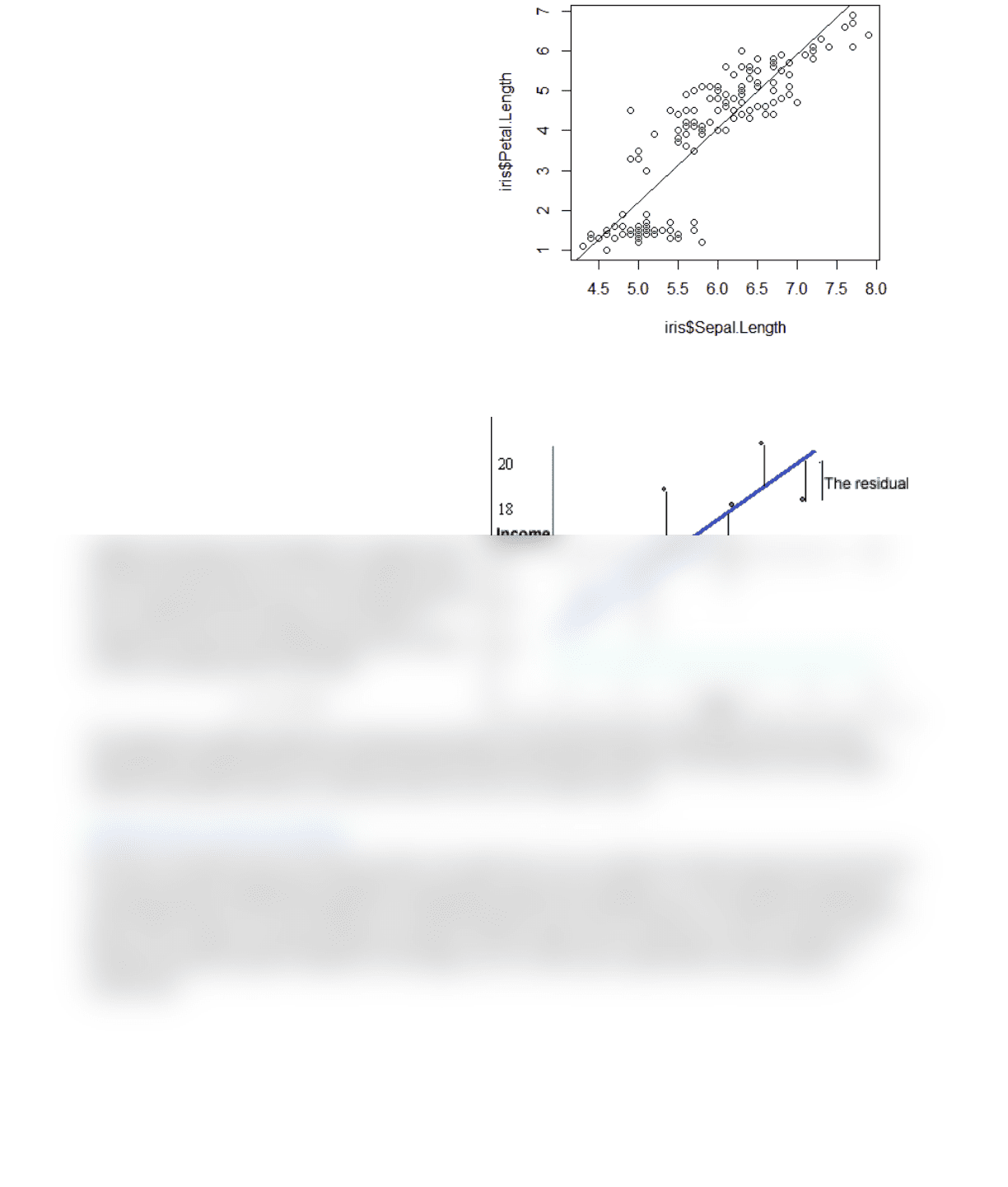
graph towards the right. Sepal length is our

independent variable plotted on the x axis while

Petal length is the dependent variable plotted on the

y axis. We are trying to quantify the effect the x

variable has on the y variable.

From the scatterplot, we can visualize that there a

positive relation between sepal length and petal

length. As sepal length increases, the petal length

increases generally. But there are anomalies to this

rule as well. These anomalies are called errors in statistical terms. Any point not lying directly on the diagonal

solid line has some error. Regression aims to find such a line where these errors are minimized.

If you look at the chart to the right, income is

regressed on the basis of age. If the blue line is the

regression line, then the vertical distance between

the line and any point is the residual/error for that

particular point. Because some of the errors can be

negative and some can be positive, we square each

residual and add them up. This way, negative errors

don’t anel the positie ones. The value we get this

way is called the sum of square errors (SSE). A

simple line is given by the following function where

a is the y intercept and b is the slope

 =  + 

The regression models change the intercept and slope in a way that the SSE in minimized. There are many

optimization methods that can be used to find the optimal intercept and slope. Two of them are the simplex

method and gradient descent. R will solve them for you so no need to worry.

Regression and causality

Be aware correlation does not equal causality. We night find a nice correlation through regression but that does

not mean that the independent variable is necessarily causing some change in y. In our example of Sepal and

petal length aoe, the to ariales are orrelated eause one auses the other. It is eause of the floer’s

genes. This is called co-variation without causality. Another similar case is when both x and y variables are

actually caused by another variable (z). If we regress y on x in this case, we get what we call a spurious

relationship.

find more resources at oneclass.com

Unlock document

This preview shows half of the first page of the document.
Unlock all 2 pages and 3 million more documents.

Already have an account? Log in

Document Summary

Regression is, in its simplest form, a technique to find the strength of relationship between a dependent (y) and independent (x). Sepal length is our independent variable plotted on the x axis while. Petal length is the dependent variable plotted on the y axis. We are trying to quantify the effect the x variable has on the y variable. From the scatterplot, we can visualize that there a positive relation between sepal length and petal length. As sepal length increases, the petal length increases generally. But there are anomalies to this rule as well. These anomalies are called errors in statistical terms. Any point not lying directly on the diagonal solid line has some error. Regression aims to find such a line where these errors are minimized. If you look at the chart to the right, income is regressed on the basis of age.

Related Questions

Question 1

Which of the following approaches to understanding and predicting consumer behavior depends primarily on the knowledge and experience of a firm's employees and its suppliers?

		Test marketing and price experiments
		Analysis of historical data.
		Direct consumer surveys.
		Expert opinion.

Question 2

In which of the following situations would reliance on expert opinion as a basis for a managerial decision be most preferred?

		When the product being marketed is relatively new.
		When the level of economic activity can have a significant effect on the demand for the firm's output.
		When the product can be packaged with a variety of price and quality combinations.
		When the business in question serves as a supplier of inputs to other businesses, especially in multi-product situations where other strategies may be prohibitively expensive.

Question 3

The approach to analyzing consumer behavior that asks consumers to rank and choose among different product attributes to reveal their relative valuation of different characteristics is called:

		conjoint analysis.
		contingent valuation.
		the hedonic estimation technique.
		a direct consumer survey.

Question 4

All of the following are limitations of direct consumer surveys except:

		the possibility of response biases because survey respondents may not want to reveal their true preferences.
		the possibility that the type of questions asked may unintentionally bias the respondent's answers.
		the likelihood that respondents will deliberately and systematically mislead interviewers.
		the possibility that consumers' responses may not reflect their actual behavior in the market place.

Question 5

Which of the following approaches to understanding and predicting consumer behavior does not actually solicit any information from potential customers?

		Expert opinion.
		Test marketing.
		Analysis of historical data.
		Conjoint analysis.

Question 6

Data collected on a sample of individuals with different characteristics at a specific point in time are called:

		panel data.
		cross-section data.
		time series data.
		none of the above.

Question 7

Which of the following approaches to understanding and predicting consumer behavior provides the most insight into how consumers can be expected to respond in an actual market setting?

		Test marketing.
		Conjoint analysis.
		Expert opinion.
		Analysis of historical data.

Question 8

An approach to analyzing consumer behavior in which consumer reaction to different prices is analyzed in a laboratory situation or a test market is called:

		non-price experiments.
		focus groups.
		price experiments.
		none of the above.

Question 9

Data collected on the same observation unit at a number of points in time are called:

		panel data.
		time series data.
		cross-section data.
		none of the above.

Question 10

A measure of how much the coefficient would vary in regressions based on different samples is called:

		F-statistic.
		standard error of the estimated coefficient.
		t-statistic.
		partial F-statistic.

Question 11

The test statistic used to test the hypothesis of whether a regression coefficient is significantly different from zero, holding all other independent variables constant, is called a(n):

		t-test.
		F-test.
		multicollinearity test.
		autocorrelation test.

Question 12

Regression analysis that analyzes the relationship between one dependent variable and several independent variables is called:

		cluster analysis.
		correlation analysis.
		multiple regression analysis.
		simple regression analysis.

Question 13

The ratio of the regression coefficient to its standard error is called:

		F-statistic.
		t-statistic.
		coefficient of determination.
		partial F-statistic.

Question 14

The coefficient of determination will range between what values?

		-1 and +1
		0 and 1
		-3 and +3
		none of the above

Question 15

The range of values in which we can be confident that the true regression coefficient lies within a given degree of probability is called a:

		confidence interval.
		logistic regression.
		prediction interval.
		none of the above.

Question 16

The estimated regression equation is Y = 10 + 2.5X, if X =0 than the predicted value of Y is equal to

		2.5
		7.5
		12.5
		10

crimsoncamel287

Suppose that, instead of taking this test, you could either have worked and earned income or partied and had a pleasurable time. Your opportunity cost of taking the test is the

	a.	forgone working or partying, depending on which was your next best choice.
	b.	forgone work.
	c.	forgone working and partying.
	d.	test because you are taking it.

1 points

QUESTION 2

A trend is

	a.	a measure of closeness on a scatter diagram.
	b.	a general tendency for a variable to rise or fall.
	c.	the maximum value of a variable.
	d.	the difference between the maximum value of a variable and the minimum value of the variable.

1 points

QUESTION 3

A time-series graph measures

	a.	time on the y-axis and the variable or variables in which we are interested on the x-axis.
	b.	time on the x-axis and the variable or variables in which we are interested on the y-axis.
	c.	the value of one variable against the value of another variable.
	d.	the value of an economic variable for different groups in a population at a point in time.

1 points

QUESTION 4

Canada has nationalized health care, so that everyone, regardless of their ability to pay, has some access to health care. Based on this observation, Canada has decided that "everyone, regardless of their ability to pay" is the answer to what microeconomic question?

	a.	Why will we offer health care?
	b.	How will health care be produced?
	c.	For whom will health care be produced?
	d.	What type of health care will be produced and in what quantity?

1 points

QUESTION 5

As a shoe factory adds more workers, shoe production grows, reaches a maximum, and then shrinks. In a diagram that has the number of workers on the horizontal axis and the number of shoes on the vertical axis, the relationship between the number of workers and the number of shoes starts as ________ and then, after the maximum point, is ________.

	a.	positive; negative
	b.	negative; positive
	c.	linear; negative
	d.	positive; linear

1 points

QUESTION 6

Microeconomics includes the study of the

	a.	choices made by individuals and businesses.
	b.	recessions and inflation in the global economy.
	c.	aggregate effects on the national economy.
	d.	reasons why the government changes interest rates.

1 points

QUESTION 7

When Fresh Express Salads decides to mechanically pick all of its lettuce, it directly answers the ________ question.

	a.	when
	b.	for whom
	c.	how
	d.	what

1 points

QUESTION 8

Proponents of cuts in income tax rates argue that when income tax rates are cut, workers have an incentive to increase their work hours. This argument is based on the assumption that

	a.	the opportunity cost of working is negative.
	b.	the marginal cost of each additional work hour is not important to most workers.
	c.	workers are irrational.
	d.	workers make decisions based on the marginal benefit of each hour worked compared to the marginal cost of work.

1 points

QUESTION 9

A choice made by comparing all relevant alternatives systematically and incrementally is

	a.	an opportunity cost.
	b.	a benefit.
	c.	a sunk cost.
	d.	a choice on the margin.

1 points

QUESTION 10

A normative statement

i. can be tested as to whether it is true or false.

ii. is considered negative.

iii. depends on a person's values.

	a.	i, ii, and iii
	b.	iii only
	c.	i and iii
	d.	ii and iii

1 points

QUESTION 11

Normative statements

i. describe how the world is.

ii. describe how the world ought to be.

iii. depend on people's values and cannot be tested.

	a.	iii only.
	b.	i only.
	c.	ii and iii.
	d.	ii only.

1 points

QUESTION 12

In order to determine whether to major in economics, a rational individual compares the ________ of the decision.

	a.	positive benefits and normative costs
	b.	normative benefits and positive costs
	c.	marginal benefit and marginal cost
	d.	opportunity cost and the sunk cost

1 points

QUESTION 13

If x increases whenever y decreases, then x and y are

	a.	positively related.
	b.	negatively related.
	c.	not related.
	d.	related but whether positively or negatively related depends on whether the x variable or the y variable is plotted on the vertical axis.

1 points

QUESTION 14

Rational choice

	a.	is what you must give up get what you want.
	b.	is made by comparing different incentives.
	c.	making the choice.
	d.	provides the answer to only the "how" question.

1 points

QUESTION 15

Scarcity results from the fact that

	a.	choices made in self-interest rare not always in the social interest.
	b.	not all goals are desirable.
	c.	people's wants exceed the resources available to satisfy them
	d.	we cannot answer the major economic questions.

1 points

QUESTION 16

When Delta decides to quit flying to Lithuania, it directly answers the ________ question.

	a.	what
	b.	why
	c.	for whom
	d.	how

1 points

QUESTION 17

A normative statement

	a.	says what is currently believed about the way the world operates.
	b.	depends on someone's values.
	c.	cannot use the word "should."
	d.	must be tested to determine if it is correct.

1 points

QUESTION 18

Which of the following statements best describes the study of economics? Economics studies how

	a.	to organize production so that scarcity does not occur.
	b.	to create incentives so that scarcity does not exist.
	c.	firms make profits.
	d.	we make choices in the face of scarcity.

1 points

QUESTION 19

Which of the following best defines economics?

	a.	Economics teaches how to limit our wants.
	b.	Economics is concerned with prices and quantities of goods and services, both at the individual level and at the industry level.
	c.	Economics helps you earn as much money as possible.
	d.	Economics studies how to choose the best alternative when coping with scarcity.

1 points

QUESTION 20

In economics, cost is ________, and benefit is ________.

	a.	the amount of money that you pay for something; the amount of money that someone else is willing to pay you
	b.	what you are willing to pay on the margin; what the government pays you when you are unemployed or retired
	c.	what you must give up to get something; what you are willing to give up to get it
	d.	the amount of money that you pay on the margin; the amount of money that you receive on the margin

1 points

QUESTION 21

If Jessie studies economics for two hours instead of going to the movies with her friends, then

	a.	the opportunity cost of studying is the missed movie.
	b.	Jessie is ignoring a sunk cost
	c.	Jessie is not responding to any incentives.
	d.	Jesse definitely is making a rational choice.

1 points

QUESTION 22

Going skiing will cost Adam $80 a day. He also loses $40 per day in wages because he has to take time off from work. Adam still decides to go skiing.

	a.	The $80 price of skiing is a sunk cost and so did not affect Adam's decision.
	b.	He loses a total of $120 per day, so his decision is irrational.
	c.	His decision is rational if Adam's marginal benefit of spending a day skiing is greater than his marginal cost.
	d.	Adam's lost $40 per day in wages is a sunk cost and so did not affect his decision.

1 points

QUESTION 23

If a curve falls and then rises, it

	a.	has a maximum.
	b.	has a linear relationship.
	c.	has a minimum.
	d.	has a constant slope relationship.

1 points

QUESTION 24

In 2003, Michael Jordan decided to retire from professional basketball. Which of the following was an opportunity cost of his decision?

	a.	the avoidance of pain and injury from playing one more year
	b.	the time he could spend with his family while retired
	c.	the lost salary from playing one more year
	d.	the value of new employment opportunities that would await him

1 points

QUESTION 25

Which of the following statements is a normative statement?

	a.	Military spending as a percent of government spending decreased by 5 percent in the 1990s.
	b.	Every American household should have health care insurance coverage.
	c.	Welfare reform has decreased the amount the government spends on welfare.
	d.	The price of computers fell last year.

greencat417

ECON 6306 Lecture Notes - Lecture 6: Scatter Plot, Spurious Relationship, Statistical Significance

Document Summary

Get access

Related Documents

STA221H1 Lecture Notes - Lecture 9: Observational Error, Dependent And Independent Variables, Blood Type

SOC202H1 Lecture Notes - Linear Regression, Scatter Plot, Linear Equation

S W 318- Midterm Exam Guide - Comprehensive Notes for the exam ( 14 pages long!)

Related Questions