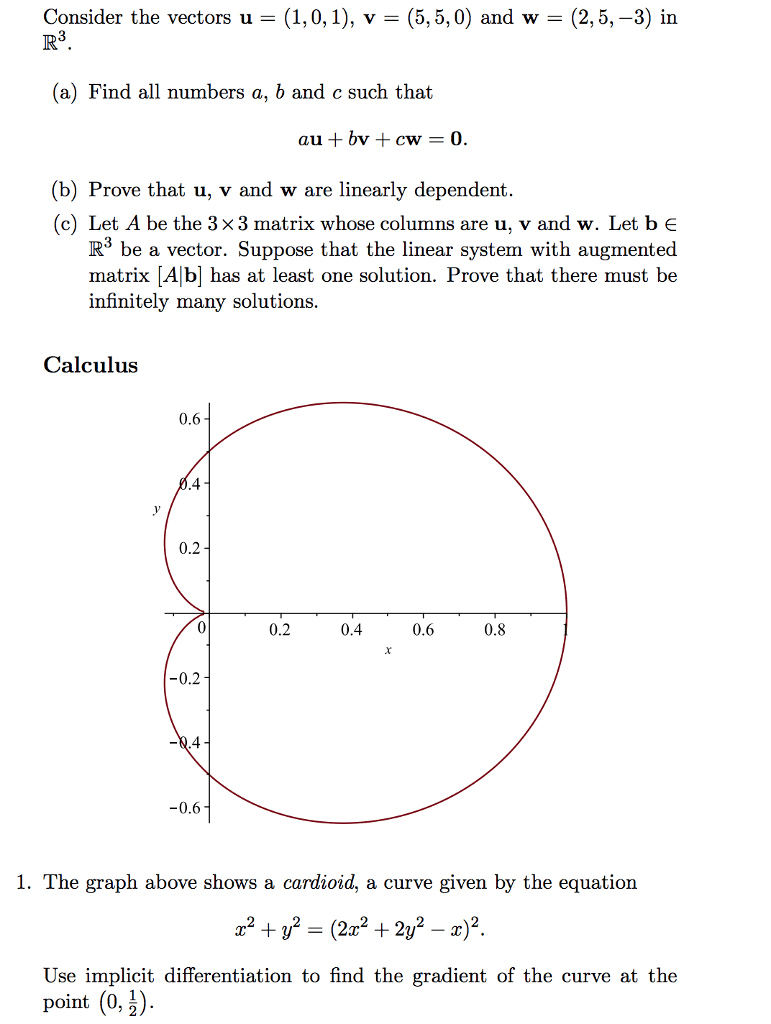
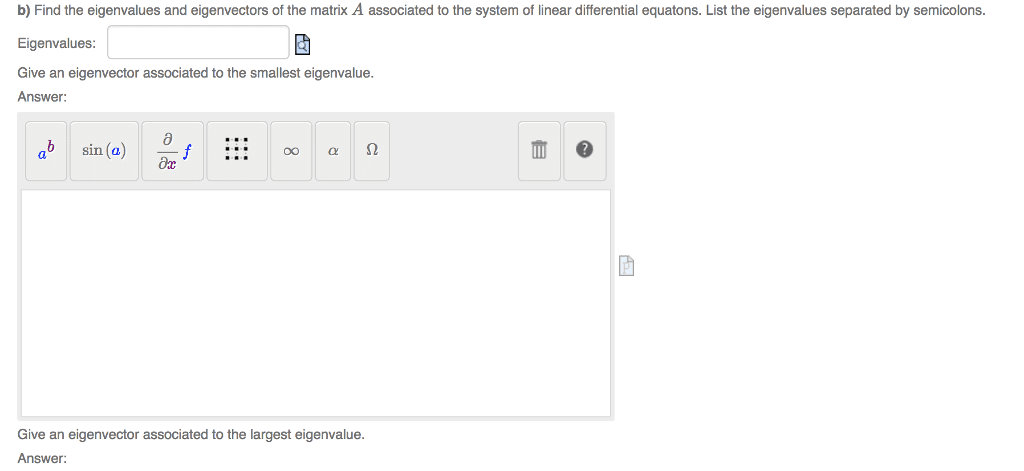
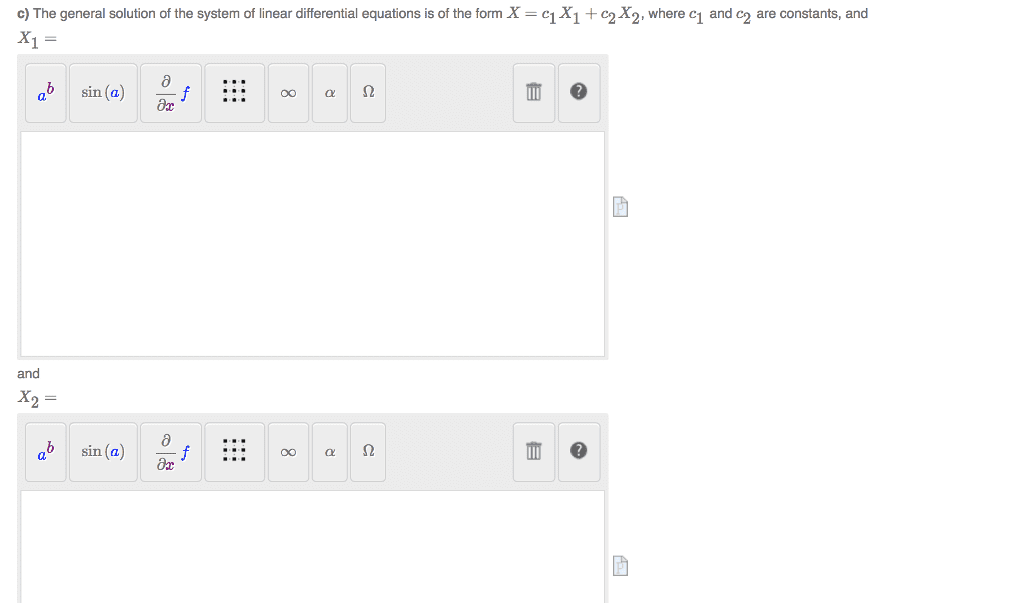
MTH 235 Lecture Notes - Lecture 31: Nonlinear System, Attractor
Document Summary
1: let the linearization at the critical point x0 of the non-linear system be u" = a0 u. 2: let the linearization at the critical point x0 of the non-linear system be u" = a0 u. 3: let the linearization at the critical point x0 of the non-linear system be u" = a0 u. Characterize the type of critical point as attractor, repeller, saddle, or center: let the linearization at the critical point x1 and x2 of the non-linear system be u" = a1 u, and u" = a2 u respectively. Find the eigenvalues + and - of matrices a1 and a2. 4: let the linearization at the critical point x0 of the non-linear system be u" = a0 u. Find the eigenvalues 0+ and 0- of matrix a0. Characterize the type of critical point as attractor, repeller, saddle, or center: let the linearization at the critical point x1 of the non-linear system be u" = a1 u.