MATH148 Lecture Notes - Lecture 28: Ratio Test, Joule
5 May 2016
School
Department
Course
Professor
Document Summary
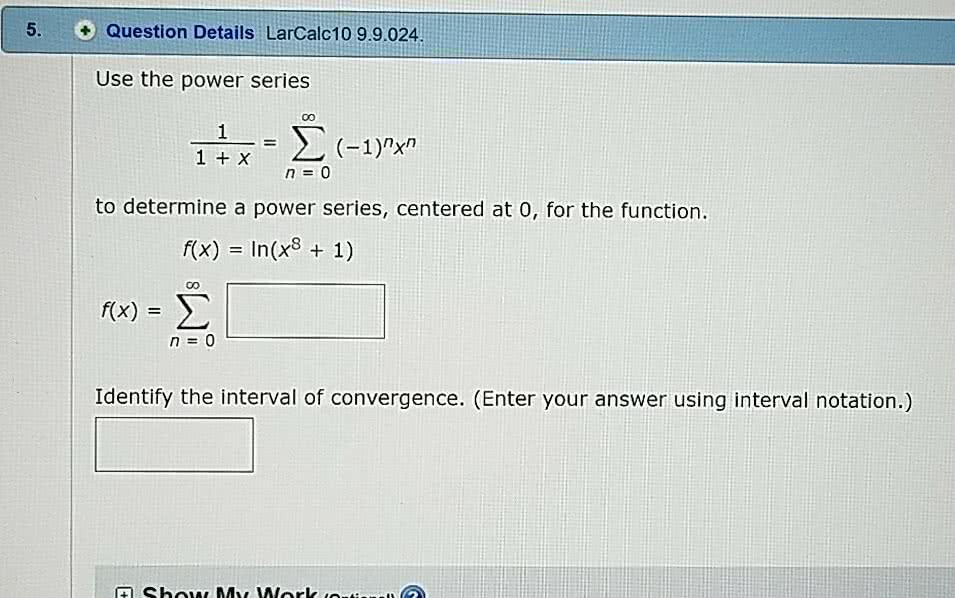
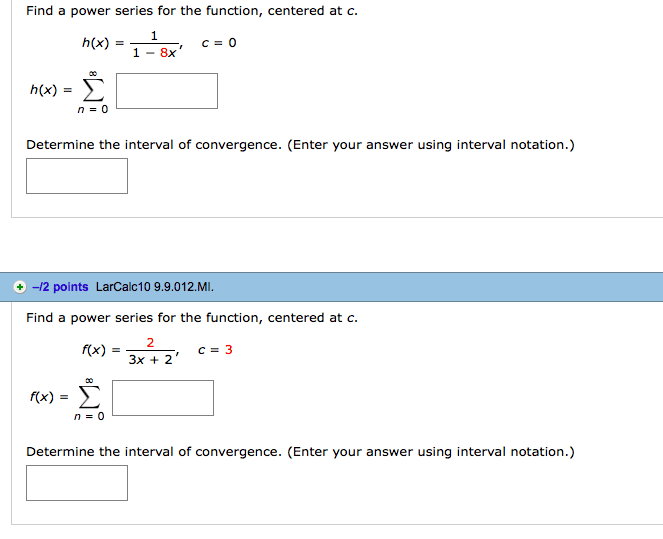
Power series are basically like in nitely long polynomials: a power series in the variable x and centered at a is the in nite series. X n=0 cn(x a)n = c0 + c1(x a) + c2(x a)2 + c3(x a)3 + + cn(x a)n + Representing functions using power series: the taylor series of a function f (x) that is centered at x = a is the in nite series f (x) = 3: the maclaurin series of a function is its taylor series centered at a = 0, the maclaurin series for some basic functions. These are very important exam- ples, so you must memorize them. (a) 1 (d) ex = 1 + x n=0 xn = 1 + x + x2 + x3 + X3 (b) sin(x) = x (c) cos(x) = 1 x2. Note: if you remember the series for sin(x), then the series for cos(x) can be obtained by simply taking its derivative.
