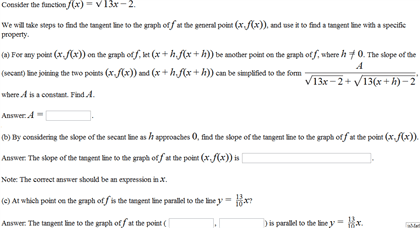MATH137 Lecture Notes - Lecture 5: Limit Point, Algebraic Function, Paula Smith

• School: University of Waterloo
• Department: Mathematics
• Course: MATH137
• Professor: Catherine Briggs

Document Summary

Let f(x) = 2x3 5x and a = 1; it follows that f( 1) = 2 + 5 = 3. The slope of the straight line joining them, bf af ab. , is the average rate of change: as we replace b with x and let x a, we obtain the instantaneous rate of change, which is just af lim x a xf af ax. Derivative of a function considered as a function: derivative function, notice that in the limit definition af lim. 0 h haf h af the point a could be any value. Thus we can derive a new function, x f lim. - or even df or dxf: the first form, f (x), is shorter; the second, df dx. If a function f is differentiable at a, it is continuous at a. Proof: given f is differentiable at a, we want to show that af xf xf af ax so af lim x a xf ax.