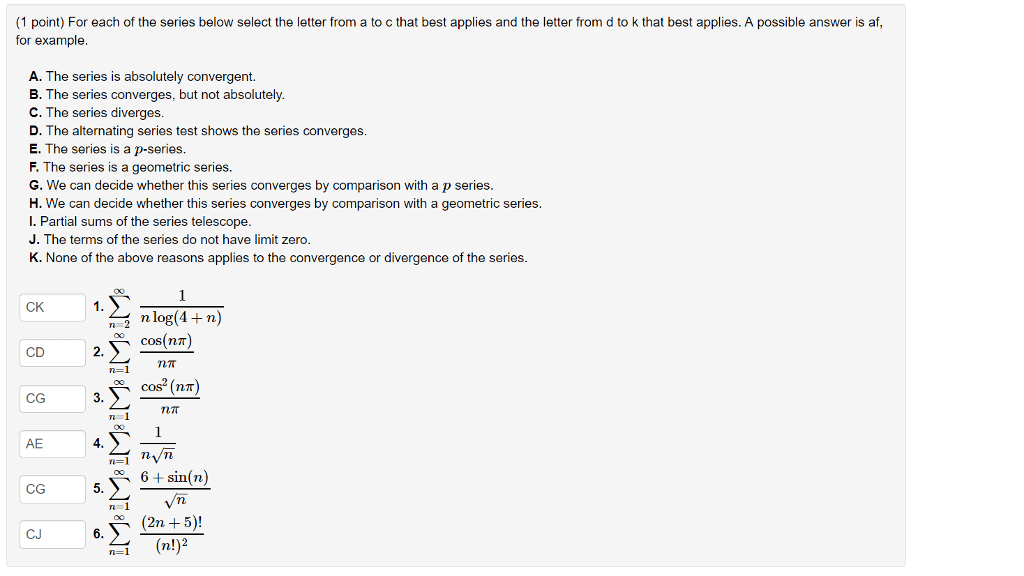
MATH118 Lecture Notes - Lecture 2: Integral Test For Convergence, Ibm System P, Ratio Test
Document Summary
Below are some formulas you may nd useful. You may tear this page o , but if you do, make sure you do not write any of your solutions on this page. If |r| 1 then the series diverges. n=0 rn = 1. If lim an does not exist or if n lim n an 6= 0 then p n=1 an diverges. n=n an converges if and only if the improper integral r . If f (x) is a continuous, positive, decreasing function on [n, 1), for some constant n > 0, such that an = f (n) for all n n , then the series p . Let s represent the sum of a convergent series satisfying the integral test. S then the error satis es r p-series. 1 np converges when p > 1 and diverges when p 1. n+1 f (x) dx s sn r n=1 bn are series with positive terms.