MATH 121 Lecture Notes - Lecture 7: Inta, Maxima And Minima, Quotient Rule

• School: Queen's University
• Department: Mathematics
• Course: MATH 121
• Professor: Alan Ableson

Document Summary

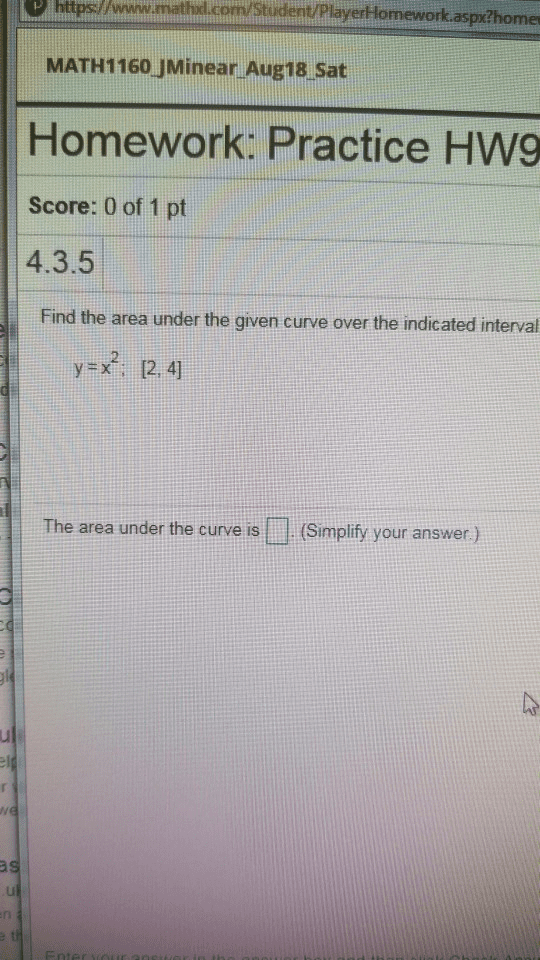
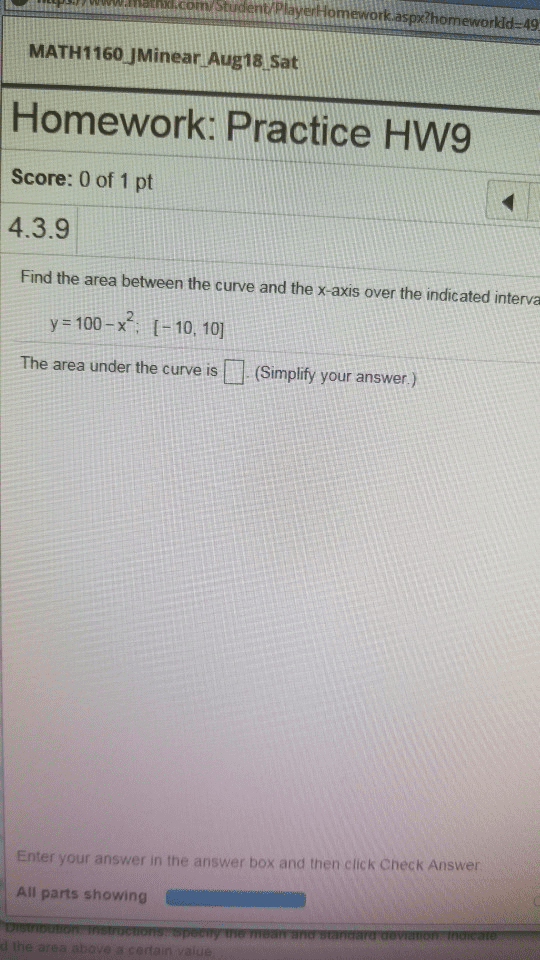
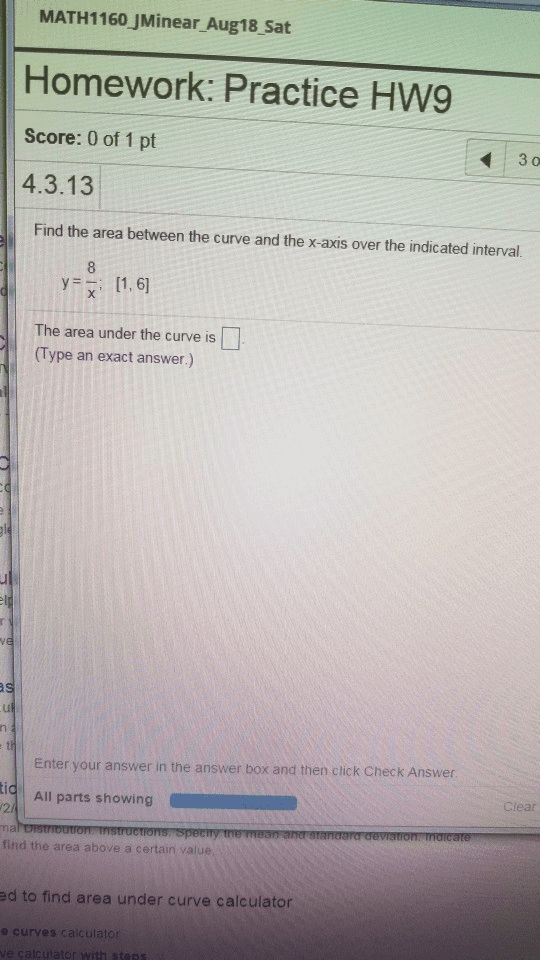
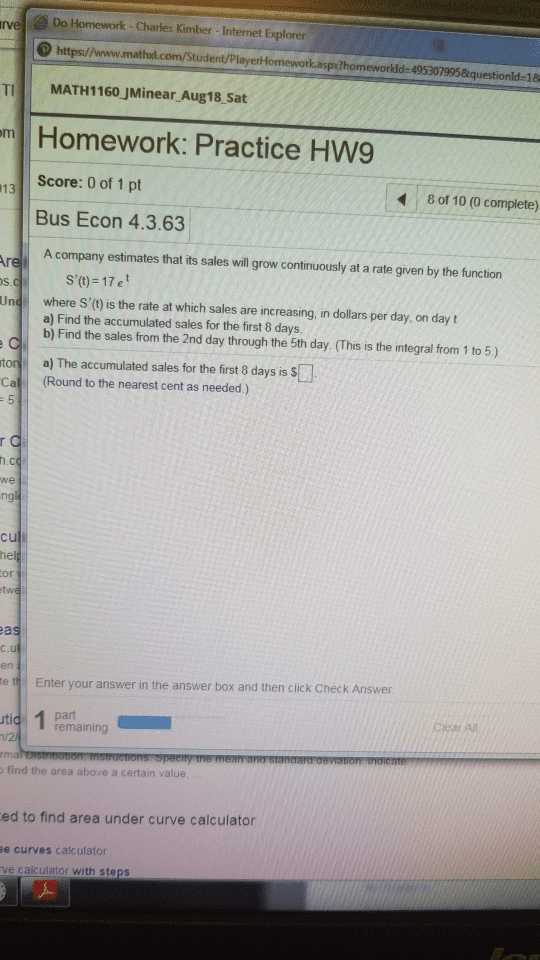
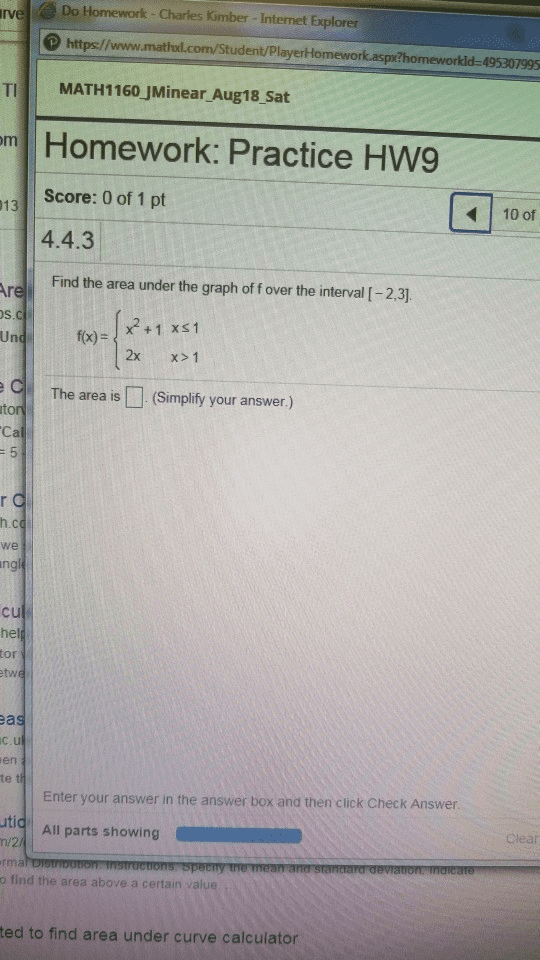
Some problems and solutions selected or adapted from hughes-hallett calculus. Setting this equal to zero and solving for x gives x = 5. [0, 1], so the global min and max values lie at the endpoints of the interval. Computation yields f (0) = 13,f (1) = 4, so the minimum is 4 and the maximum is 13: find the maximum and minimum values of the func- ln(x) x tion f (x) = on the interval [1,3]. The critical point of f (x) is the so- lution to f(cid:48)(x) = 0. The derivative isf(cid:48)(x) = x 2 ln(x) x2 . Setting this equal to zero and solving for x gives x = e1 = e. The values of the function at the endpoints of the in- terval are f (1) = 0, f (3) = 0. 3662, so the minimum value is 0, and the maximum value is 1 e = 0. 3679. e = 0. 3679.