MATH1051 Lecture Notes - Lecture 1: Quotient Rule, Antiderivative, Product Rule

4.9 – Antiderivatives
Definition of Antiderivative
● is an antiderivative of a function on interval F f I
●If you differentiate , you get the original function F f
●(x) (x)F′=f
Theorem
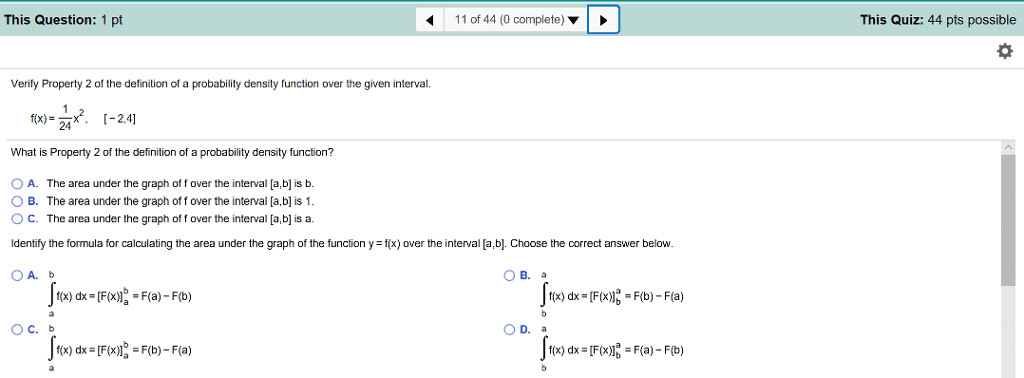
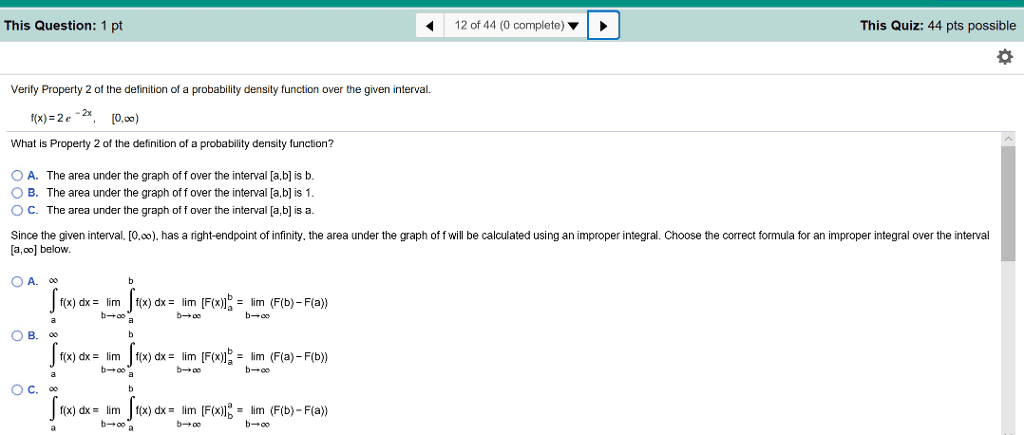
●If is the antiderivative of on , then the most general antiderivative of on isF f I f I
where is an arbitrary constant(x)F+C C
●All possible variations of constant C
Exercise
●Find the most general antiderivative of…
oA) in (x) s
▪os (x) − c+C
oB) x
1
▪n|x|l+C
oC) xn
▪x⁄(n))( n+1 +1 +C
oD) 3
1+x2
▪tan (x) 3 −1 +C
Table of Antiderivatives
(x)f′
(x)f
xn
n |x| l+C
k
xk +C
x
x+C
bx
bx
Inb
os (x) c
in x s+C
in (x) s
os x − c+C
x sec2
an x t+C
x cos2
ot x − c+C
Document Summary
, then the most general antiderivative of f. + c: a) in (x) os (x) Table of antiderivatives f (x) xn k. X bx os (x) c in (x) s x sec2 cos2 x ec xtan x s sc xcot x c. In which f (x) is a function and. Derivative rules ec x s sc x c sin 1 x cos 1 x tan 1 sec 1 x x. + c (f(x) g(x)) = f (x) g (x: addition and subtraction rule (cf(x)) = c f (x) + f (x)g (x) (f(x)g(x)) = f : constant rule (x)g(x, product rule g(x)f (x) f(x)g (x, quotient rule (g(x))g (x) (g(x))2 f(x) g(x) (f(g(x))) = f , chain rule. Find all o g g g g f f x 23 x. + x2 2 1 2 such that (x) (x) (x) g (x) cos (x) Simplify further (don"t forget the +c!) x3 2 2 x3 4 2 x (x 1 2)