MATH1051 Lecture Notes - Lecture 14: Partial Fraction Decomposition
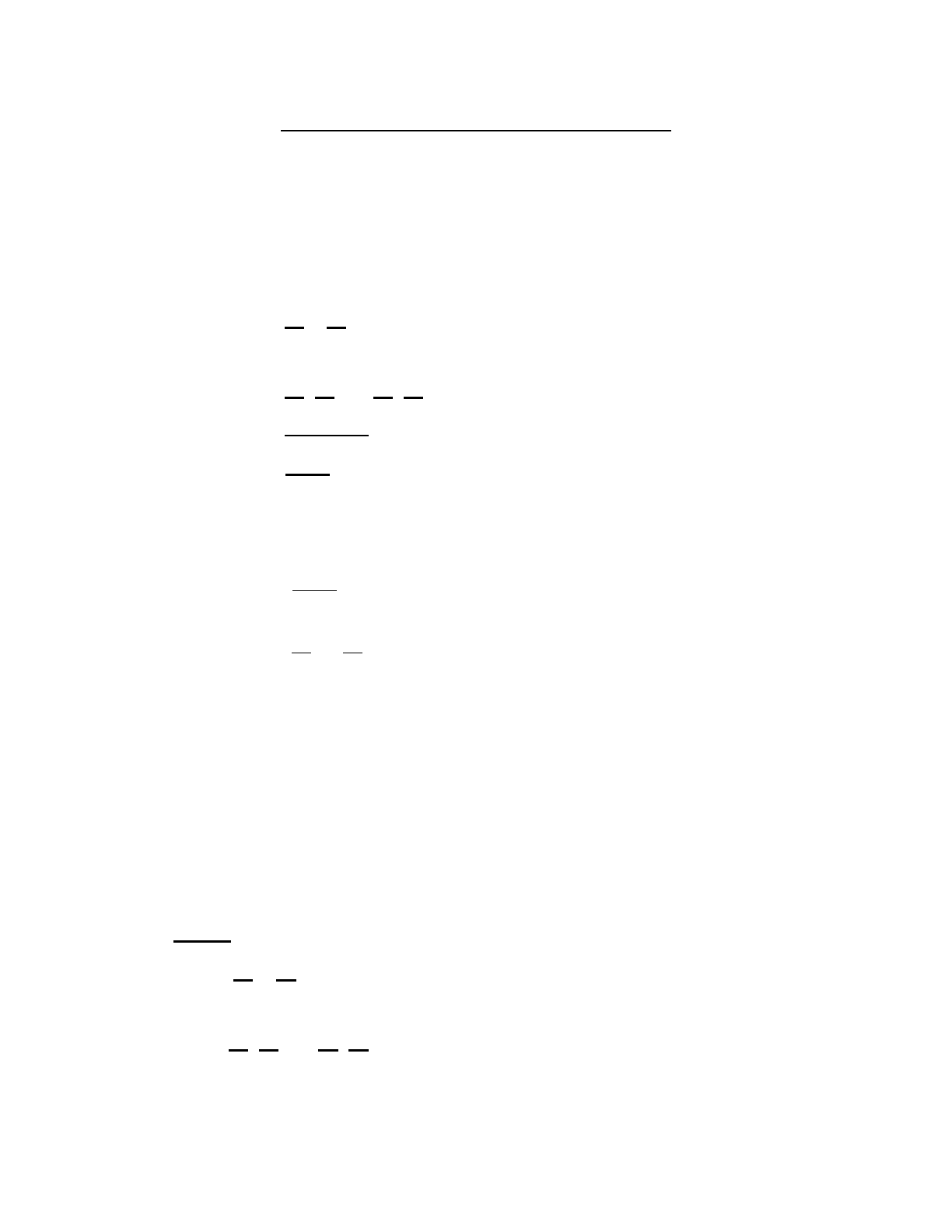
Lecture #14 – 7.4 - Partial Fraction Decomposition
What is Partial Fraction Decomposition?
●Basically, it’s like un-common denominator
●What is common denominator?
○Example #1
■3
x+1 +4
x−3
●How would we add these two fractions?
■( ) ( )
3
x+1 x−3
x−3 + 4
x−3 x+1
x+1
■(x+1)(x−3)
3(x−3) + 4(x+1)
■7x−5
x−2x−3
2
●Try another example by taking it a step further
○Example #2
■dx
∫
7x−5
x−2x−3
2
■ dx
∫
3
x+1 + 4
x−3
■ln 4ln C3x
|+ 1| + x
|− 3| +
●The goal of taking this integral is to figure out how to break down the function
○It’s not easy to get from step 1 to 2 in Example #2
○So, we’ll learn to use Partial Fraction Decomposition
Example #3
●7x−5
(x−3)(x+1)
○ A
x−3 +B
x+1
■How would we add these two?
○( ) ( )
A
x−3 x+1
x+1 + B
x+1 x−3
x−3
■Common denominator

○(x−3)(x+1)
A(x+1) + B(x−3)
■Add the two terms
○7x−5
(x−3)(x+1) = (x−3)(x+1)
A(x+1) + B(x−3)
■Realize that you can set these equal to each other
○x A(x) B(x)7 − 5 = + 1 + − 3
○x Ax A Bx 3B7 − 5 = + + −
○7)x (− ) Ax Bx A B( + 5 = + + − 3
■Group like terms
○7)x (− ) (A)x (A B)( + 5 = + B+ − 3
■You can see the parallels here
■Then we can create equations to solve for A and B
○ A7 = + B
■ 7A= − B
○ A B− 5 = − 3
■ (7 ) B− 5 = − B− 3
■ 7 B− 5 = − B− 3
■B 124 =
■ 3B=
■ 4A=
●7x−5
(x−3)(x+1) = 3
x+1 +4
x−3
○Plug back in the values for A and B
Example #4
●∫
6x + 9
x + x − 2
2
○
6x + 9
x + x − 2
2= A
x+2 + B
x − 1
○(x+2)(x−1)
A(x−1) + B(x+2)
■Common denominator

○x Bx 2B 6x 9A−A+ + = +
■Set the two numerators equal
○x Bx A 2B 6x 9A+ − + = +
■Rearrange
○A B)x (− 2B) (6)x (9)( + + A+ = +
■Separate the variables so that they’re parallel
○ B 6A+ =
○ 2B 9− A+ =
■Simplify
■ 6B= − A
■ 2(6 ) 9− A+ − A=
■ 12 2A 9− A+ − =
■A − 3 = − 3
■ A= − 1
■ 5B=
●Then plug these values back in
○∫
A
x+2 +B
x−1
○− dx
∫
1
x+2 + 5
x−1
Example #5
●dx
∫
6x − 35
2x − 5x − 12
2
○6x − 35
(2x+ 3)(x−4)
■Unfoil the denominator first
○
A
(2x + 3) + B
(x − 4)
■Then prepare the partial fraction
○( ) ( )
A
2x+3 x−4
x−4 + B
x−4 2x+3
2x+3
■Combine the two using common denominators
Document Summary
Lecture #14 7. 4 - partial fraction decomposition. How would we add these two fractions? x 3 + 4. Try another example by taking it a step further. The goal of taking this integral is to figure out how to break down the function. It"s not easy to get from step 1 to 2 in example #2. So, we"ll learn to use partial fraction decomposition. How would we add these two? x+1 + b. Realize that you can set these equal to each other. Then we can create equations to solve for a and b. Plug back in the values for a and b. A(x 1) + b(x+2) x+2 + b x 1 (x+2)(x 1) Separate the variables so that they"re parallel. A (2x + 3) + b (x 4) Combine the two using common denominators x 4 + b. Plug in the value of a from the first equation into the second. Plug in the values for a and b.


