MATH1115 Lecture 5: Limit of a function, Limit Laws and Continuity

64 views2 pages

whitegoat396

30 May 2018

School

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

MATH1115: Limit of a function, Limit Laws and Continuity

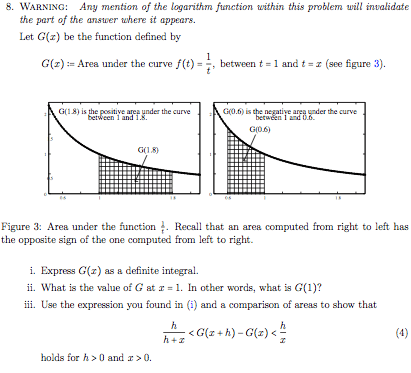
● Limit of a Function:

○ Suppose that f is a real-valued function defined on an interval which

includes a, expect that f might not be defined at a itself.

○ Then we say that the limit of f(x) as x approaches a equals L, and write lim

x->a f(x) = L, if the value L can be approximated as precisely as desired

using f(x), simply by requiring that x is sufficiently close to a without

equalling a [how close this is can depend on the level of precision

required]

○ Can talk about the limit as x -> a- f(x) from the left and ignore the

behaviour on the right hand side and x-> a+ f(x) from the right and ignore

the behaviour on the left hand side and see limiting behavior

● Limit Laws:

○ Assuming that lim x-> a f(x) = L and lim x-> a g(x) = M

■ Lim x->a [f(x) + g(x)] = L + M

■ Lim x->a [f(x) - g(x)] = L - M

● Proof: by i. Lim x->a (-g(x)) = -M , lim x->a [f(x)-g(x)] = lim x-

>a [f(x) + g(x)] = L + -M = L - M

■ Lim x->a [cf(x)] = cL

■ Lim x-> [f(x)g(x)] = LM

■ If M doesn’t = 0 then lim x->a [f(x)/g(x)] = L/M

■ If nEN, then lim x->a [f(x)]n = Ln

■ Lim x->a c=c

● C is not dependant on X

■ Lim x->a x=a

■ Lim x-> a xn=an

● Special case of Law 6 applied to Law 8

■ If nEN, then lim x->a nsqrt(x) = nsqrt(a)

● If n is even we assume a>0

■ If nEN, then lim x->a nsqrt(f(x)) = nsqrt(L)

● More general case of Law 10

● If n is even we assume L > 0

○ E.g. Lim x->0 (sqrt(1+x) -1)/x thus we are not allowed to use the limit law

of 5 aka L/M rule

■ F’(0) where f(x) = sqrt (1+x)

■ Lim h->0 (sqrt (1+h) - 1)/h

■ Lim h->0 [f(0+h) - f(0)]/h <- first principle

■ Lim x->0 [(sqrt(1+x)-1)(sqrt(1+x)+1)] / x(sqrt(1+x)+1)

■ Lim x-> 0 1+x-1/x(sqrt(x+1) + 1)

find more resources at oneclass.com

Unlock document

This preview shows half of the first page of the document.
Unlock all 2 pages and 3 million more documents.

Already have an account? Log in

Document Summary

Math1115: limit of a function, limit laws and continuity. Suppose that f is a real-valued function defined on an interval which includes a, expect that f might not be defined at a itself. Assuming that lim x-> a f(x) = l and lim x-> a g(x) = m. Lim x->a [f(x) + g(x)] = l + m. Lim x->a [f(x) - g(x)] = l - m. Proof: by i. lim x->a (-g(x)) = -m , lim x->a [f(x)-g(x)] = lim x- >a [f(x) + g(x)] = l + -m = l - m. If m doesn"t = 0 then lim x->a [f(x)/g(x)] = l/m. If nen, then lim x->a [f(x)]n = ln. Special case of law 6 applied to law 8. If nen, then lim x->a nsqrt(x) = nsqrt(a) If nen, then lim x->a nsqrt(f(x)) = nsqrt(l) If n is even we assume l > 0.

Related Questions

Hello,

Theproblem asks:
For what values of constants a andb is the function f(x) continous on (-infinity, + infinity) ?

x + 2 , x < 1
f(x) = a , x = 1
bx^2 , x > 1

If you have time, please read below and confirm or correct mythinking on this problem:

To me the problem is saying:

That as the limit of x approaches 1 from the left(1-) and/or from the right (1+); f(x) =3.

So, for the limit to be continuous, f(x) = 3 it will haveto be true [when x is/close to 1]for each of the three (piecewiseequations? what is the correct terminology?).

So I think that means a = 3 and b = 3 when x = 1 or xapproaches 1. To check this mathematically, do I solve for eachvariable? I.e. 3 = bx^2 and 3 = a?

Am I understanding this problem correctly? If you havetime, please explain (in writing) what this problem means and howto solve it.

Thanks!