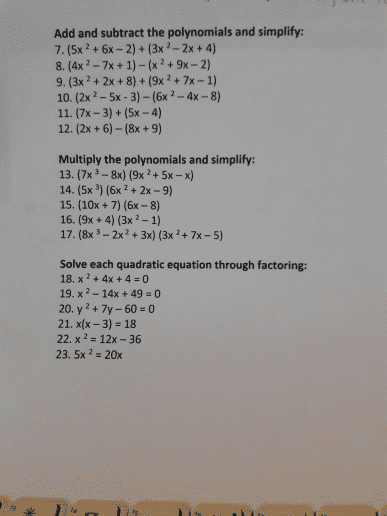Question

Solve the equation. Log_4 (x + 2) + log_4 (x - 4) = 2 7 6 6, -4 -4 Rewrite the expression in terms of log(2) and log(5). Log(1000) 3 log(2) + log(5) 3 log(2) - 3 log(5) (3 log2)(3 log5) 4 log(2) + 3 log(5) Write the expression as a single logarithm with coefficient of 1. Assume that all represent positive real numbers. 5 log3 (5x - 6) + 6 log3 (6x + 3) log3 (5x - 6)^5/(6x + 3)^6 log3 ((5x - 6)^5 + (6x + 3)^6) log3 (5x - 6)^5 (6x + 3)^6 30 log3 (5x - 6)(6x + 3) Solve the system by addition method. x^2 + y^2 = 116 x^2 - y^2 = -84 ((4, 10), (10, 4), (-4, -10), (-10, -4)) ((4, 10), (-4, 10), (4, -10), (-4, -10)) ((4, -10), (4, 10)) ((-4, -10), (-10, -4)) out the first five terms of the sequence. a_n = 2/n^2 1/4, 2/9, 3/16, 4/25, 5/36 1, 1/2, 1/3, 1/4, 1/5 1, 1/4, 1/9, 1/16, 1/25 2, 1/2, 2/9, 1/8, 2/25 Evaluate the summation. sigma_i = 4^7 (26) 44 14 30 22 Use the compound interest formulas A = P(1 + r/n)^nt and A = Pe^rt to solve. Find the accumulated value of an investment of $9000 at 9% interest rate compounded continuously for 3 years. $10, 160.00 $10, 360.23 $10, 479.72 $10, 579.72