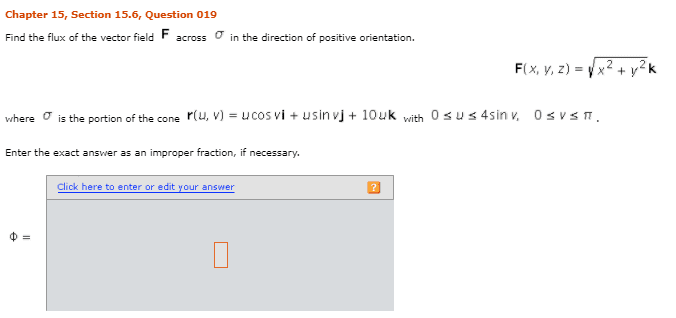
#5 please
normal vector (a) F(z,y, z) " (2z, 2y, 2), s is the sphere rı + va + (b) 9 F(z, y,z)=(r,y,z), sÃs the clond surfice r"Var+ã¢,2-4 ban/ (c) F(a, v. ) (', ), S is the surface of the cube bounded by the three coordinste planen and the three 2 planes z-2, y-2 and (d) P(a, y,e)- (r, a), s is the cloeed surface having sides the coordinate planen and the plane with equation (e) F(z, y, s) = (y3 + ra, ra + ra,z? + yay and S is the surface 4z? + 9V2 + 25zs_ 900 () F(a.v.) (g) F(z, y, z) (r),-6), in the surfuce of (ys tan-1 (Ñг + r2)-2r,mer-"-2y, sin(z2 + v) + 5z), s is the sphere of radius 1 centered at the origin (h) F(r,y,a) (2 +9,2y +2,2 +2), S is the closed surface 2+y-9 with oSz3 (0) F(r, y,z)-,), S is the boundary of the solid cylinder+-1,0s s1 4r 4. Let S'be the surface9. Compute Fnds, where F(e,.) and n is the outward unit normal. 5. Let S be the surface parametrized by 0 u S 3, and O 2m, r(u,v)-|u cos(v), usin(v), u). Suppose f(z, y, z) v is a twice continuously diferentiable function. ComputeP nds, where F),-1) and n is the outward unit normal. ,0 6. Let be the surface parametrized by r(u, v) (2 sin(u) cos(v), 2 sin(u) sin(v), 2 cos(u)),0 21. u Evaluate F . nds, where F(z, y, z) = (2rs_ 2y,4x3-4zy, 1) and n is the outward unit normal.
Show transcribed image text normal vector (a) F(z,y, z) " (2z, 2y, 2), s is the sphere rı + va + (b) 9 F(z, y,z)=(r,y,z), sÃs the clond surfice r"Var+ã¢,2-4 ban/ (c) F(a, v. ) (', ), S is the surface of the cube bounded by the three coordinste planen and the three 2 planes z-2, y-2 and (d) P(a, y,e)- (r, a), s is the cloeed surface having sides the coordinate planen and the plane with equation (e) F(z, y, s) = (y3 + ra, ra + ra,z? + yay and S is the surface 4z? + 9V2 + 25zs_ 900 () F(a.v.) (g) F(z, y, z) (r),-6), in the surfuce of (ys tan-1 (Ñг + r2)-2r,mer-"-2y, sin(z2 + v) + 5z), s is the sphere of radius 1 centered at the origin (h) F(r,y,a) (2 +9,2y +2,2 +2), S is the closed surface 2+y-9 with oSz3 (0) F(r, y,z)-,), S is the boundary of the solid cylinder+-1,0s s1 4r 4. Let S'be the surface9. Compute Fnds, where F(e,.) and n is the outward unit normal. 5. Let S be the surface parametrized by 0 u S 3, and O 2m, r(u,v)-|u cos(v), usin(v), u). Suppose f(z, y, z) v is a twice continuously diferentiable function. ComputeP nds, where F),-1) and n is the outward unit normal. ,0 6. Let be the surface parametrized by r(u, v) (2 sin(u) cos(v), 2 sin(u) sin(v), 2 cos(u)),0 21. u Evaluate F . nds, where F(z, y, z) = (2rs_ 2y,4x3-4zy, 1) and n is the outward unit normal.